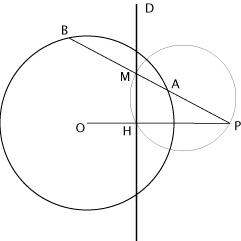
Définition :
Deux points M et P sont dits conjugués par rapport à un cercle lorsqu'ils sont conjugués harmoniques par rapport aux points A et B où la droite MP coupe le cercle.

Le cercle de diamètre MP est alors orthogonal au cercle de centre O de rayon R.
Définition :
Le lieu des conjugués d'un point P par rapport à un cercle O est une droite D perpendiculaire à OP appelée polaire de P par rapport au cercle O.
Définition :
Le point P qui admet la droite D pour polaire est le pôle de la droite D.
Propriétés :
La polaire d'un point P par rapport à un cercle O est la transformée dans l'homothétie (P, 2) de l'axe radical du cercle O et du cercle point P.
La polaire du point P est l'axe radical du cercle O et du cercle de diamètre OP.
La polaire du point P extérieur au cercle O joint les points de contact des tangentes au cercle issues de P.
Le pôle d'une sécante EF est le point d'intersection des tangentes en E et F.
Propriété fondamentale :
Lorsque la polaire d'un point P passe par un point M, la polaire de M passe par P.
Corollaires :
Les polaires des points d'une droite concourent au pôle P de cette droite.
Les pôles des droites issues d'un point P sont alignés sur la polaire du point P.
Les polaires a, b, c, d de quatre points A, B, C, D formant une division harmonique forment un faisceau harmonique.

Définition :
Deux droites D et D' sont conjuguées par rapport à un cercle O si leurs pôles P et P' sont conjugués par rapport au cercle O.
Les conjuguées d'une droite D sont les droites issues de son pôle P