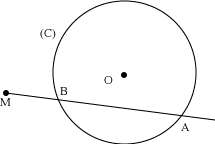
Fig. 1 - Puissance d'un point
Définition :
soient A et B les intersections avec un cercle (C) de centre O, d'une droite (D) issue de M. La puissance de M par rapport au cercle (C) est le produit :
Si M est extérieur à (C), PO(M) > 0. Si P est intérieur à (C), PO(M) < 0. Si P est sur (C), PO(M) = 0.
Soit d la distance OM, R le rayon de C, PO(M) = d2 - R2
Définition :
soient deux cercles (C) et (C'), le lieu des points qui ont même puissance par rapport aux deux cercles (C) et (C') est l'axe radical (D) des deux cercles.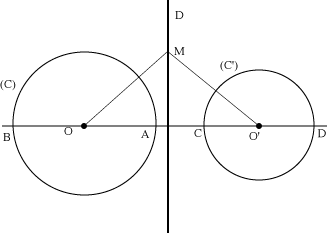
Si les deux cercles sont concourants, l'axe radical est leur corde commune.
Si les deux cercles sont tangents, l'axe radical est leur tangente commune.
Théorème :
les axes radicaux de trois cercles pris deux à deux concourent en un point qui a même puissance par rapport aux trois cercles et qu'on appelle centre radical des trois cercles.Théorème :
La différence des puissances d'un point par rapport à deux cercles est égale au double produit de la distance de leurs centres par la distance du point à leur axe radical.