J'ai découvert les logarithmes en classe de première et ai aussitôt compris les énormes possibilités de calcul qu'ils offraient. Je ne connaissais pas encore la règle à calcul qui en est une application concrète et qui allait me servir pendant toutes mes études.
Trouvant la consultation des tables fastidieuses, j'avais imaginé une machine où la table serait écrite sur un long ruban qu'un moteur déroulerait et enroulerait jusqu'à la ligne qui nous intéresserait.
Je n'avais pas pensé que l'électronique naissante permettrait un jour de calculer instantanément la valeur cherchée et pour un coût dérisoire.
La fabrication des tables elles mêmes, à cette époque pré-informatique, me laissait perplexe. Je ne sais d'ailleurs toujours pas comment elle étaient établies à l'époque.
Avec la fréquence d'utilisation de log(2) et log(3), j'avais trouvé économique de connaitre ces valeurs par cœ;ur : 0,30103 et 0,47712 et je ne les ai pas oubliées !
Bien entendu de nos jours une table de logarithmes ne sert à rien et personne ne pense à en emporter une dans ses déplacements. Mais si on pouvait être dans la situation d'en avoir besoin et de ne pas en avoir sous la main, je prétends qu'on peut s'en constituer une facilement.
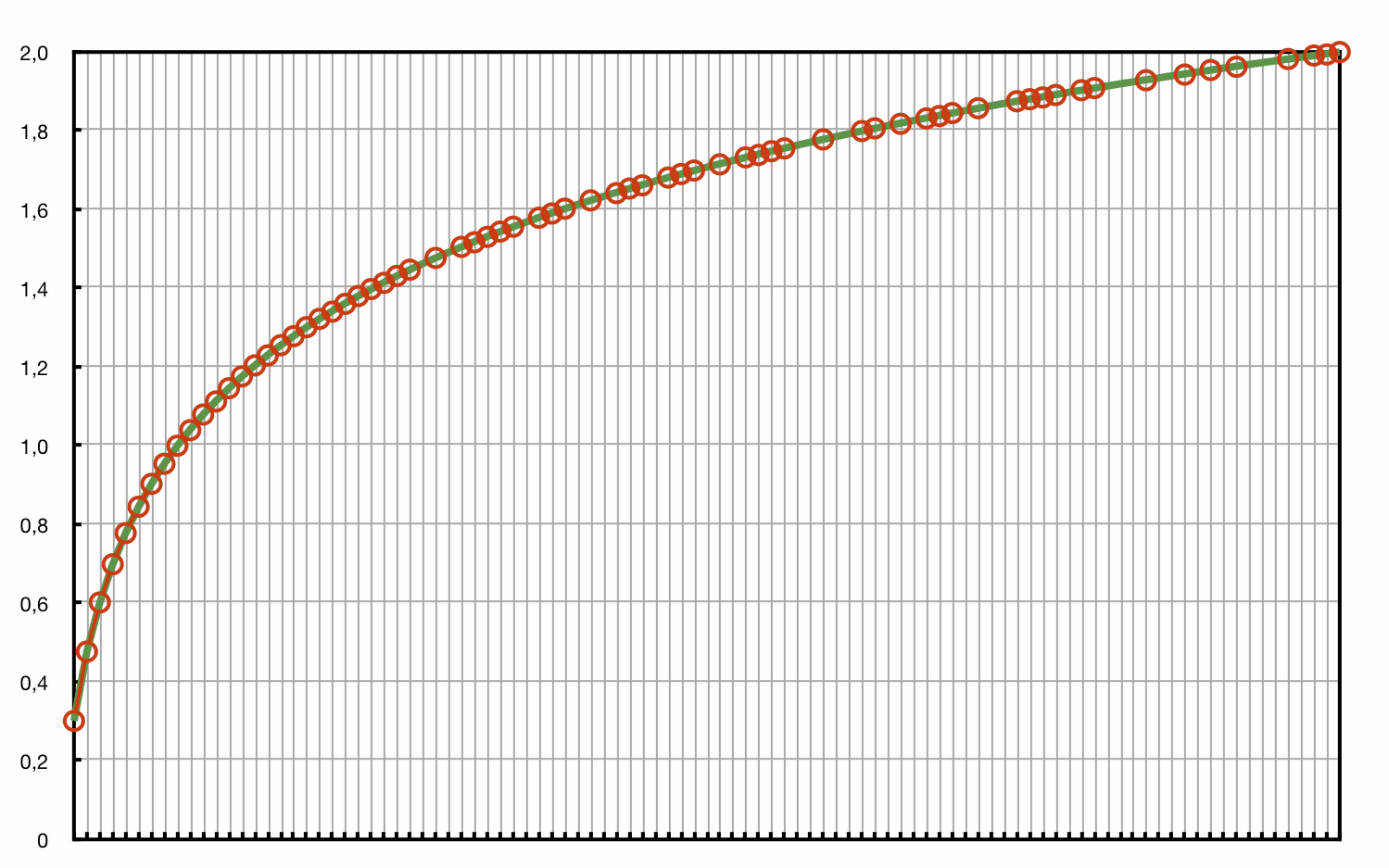
Sous la réserve bien sûr d'avoir en mémoire les deux valeurs 0,30103 et 0,47712, on peut par combinaison trouver les autres. J'ai ainsi entrepris d'évaluer les valeurs entre 1 et 100 et sur la figure ci-dessous (pas tout à fait complète mais suffisante pour se faire une idée), la courbe verte est la courbe log tandis que les ronds orangés sont les valeurs calculées à partir de 0,30103 et 0,47712
La manière de procéder est la suivante. Entre 1 et 10 on a :
- 1 qui donne 0
- 2 connue
- 3 connue
- 4 c'est 2 log(2)
- 5 c'est 1 - log(2)
- 6 c'est log(2) + log(3)
- 8 c'est 3 log(2)
- 9 c'est 2 log(3)
- 10 qui donne 1
Il manque 7 comme c'est un nombre premier, on n'a aucune chance de trouver une évaluation par combinaison. Reste l'interpolation :
Mais plutôt qu'écrire log(7) = (log(6) + log(8) / 2, je préfère log(49) = (log(48) + log(50)) / 2.
Ensuite log(7) = log(49) / 2
Quant à log(48) c'est 4 log(2) + log(3) et log(50) c'est 2 - log(2)
L'interpolation linéaire entre 48 et 50 est bien meilleure qu'entre 6 et 8 :
ainsi log(7) calculé par log(6) + log(8) est égal à 0,994701 de la vraie valeur
tandis que calculé par log(48) + log(50), le rapport est 0,999946
on passe d'une erreur de 5 pour mille à 5 pour cent mille !
Figure tracée avec Numbers d'Apple.